One-Point Perspective

People seemed to like my first post about the fourth dimension, so I'm going to attempt to write another. This one gave me a migraine when I first started thinking about it, so be warned.

As you might remember from geometry classes, there are five "Platonic Solids" in three dimensions. These are objects that are made up of a single two-dimensional polygon, repeated and connected. In math terms, they're the tetrahedron, the cube, the octahedron, the dodecahedron, and the icosahedron. In geek terms, they're the d4, the d6, the d8, the d12, and the d20. They're named after Plato, who believed that the four elements of the universe were made up of little pieces, shaped like these solids. Water was the icosahedron, which is almost spherical and can roll around. Fire was the tetrahedron, which has sharp corners and is only stable with a point facing upwards. Earth was the cube, which can be packed together into bigger cubes without space between them. And air was the octahedron, for no real reason. (The dodecahedron was left out of this theory. It's now best known as the D&D die that nobody ever uses, the d12.)

If you think about it, these could be considered the 3-dimensional equivalents to regular polygons--shapes where every edge is the same length, such as a square or an equilateral triangle. So could there be four-dimensional equivalents, built out of 3-dimensional solids?

The easiest one to think about is the cube, so I'll just focus on that one for now.

The cube can be thought of as part of a series, going up through dimensions: in one dimension there's the line segment, in two dimensions the square, in three the cube, and...so on? The four-dimensional one is sometimes called the 4-hypercube, or tesseract.

Now, if you start from the one-dimensional line segment, you can form a square by duplicating the segment, then connecting them. So if we start with a one-inch line segment pointing forward-backward, we can place another segment an inch to the right, and connect the endpoints.

That gets a square. And we can repeat the process to make a cube: place another square an inch above the first, and connect the endpoints.

To make a tesseract, then, it would seem that you could just place another cube one inch along the fourth dimension, and connect the lines. That makes theoretical sense...but what would it look like, if you actually created one? To figure that out, we can turn to perspective.

Generally perspective is used to portray a three-dimensional object in two dimensions, by stretching and skewing parts of it.

If we took a folded paper cube, made of six squares, we could show it to a Flatland being by placing the six squares next to each other--"unfolding" it into a cross shape.

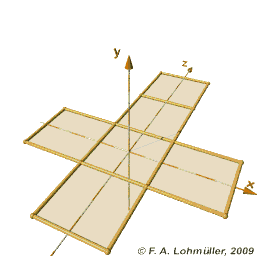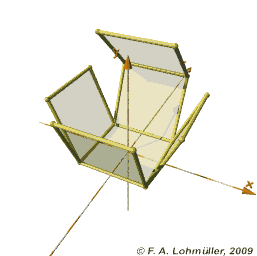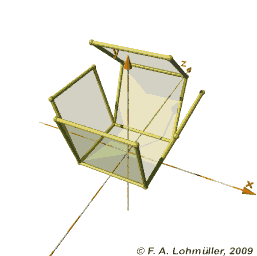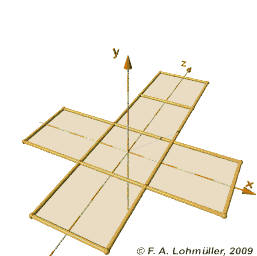I didn't make this image, I'm bad at 3d animation.

And we can do the same for the eight cubes of the tesseract.

Nor this one, sorry.

Salvador Dali once made a painting based on this net.

But this picture doesn't help us very much. I, for one, can't really tell anything about what the finished tesseract would look like from seeing the arrangement of cubes there, even though I can see what shapes comprise it.

So the other way to show it to the Flatlanders would be to use perspective.

If you look at the picture, you can imagine the cubes being there, although of course it's two-dimensional. But if you tell the Flatlanders that each cube made of six squares, they will probably be very confused. Looking at the picture, one can see six rhombuses, but only two actual squares (the front and back). The other four are distorted by the perspective. And if you somehow animated your drawing to make the cube rotate, it would blow their minds. Somehow these squares are becoming rhombuses, and passing through each other, and even changing in size! But somehow this is supposed to be a solid object?

If it doesn't rotate, click it. Note: I didn't make this!

It might be easiest to draw the cube with perspective using one-point perspective, where every line leads to a single vanishing point. [The cube on the right.]

You can still see that this is a cube, although it's less clear than some other ways of drawing it.

I was thinking a few days ago that this form of perspective could also possibly be applied to a four-dimensional object. One-point perspective is probably the easiest to make. But somehow it will need to be applied to a three-dimensional object...

Looking at the cube, it looks like a smaller square inside a bigger square, with diagonal lines representing the third dimension.

So, why not try that with our tesseract?

Unfortunately, I can only upload two-dimensional pictures onto this blog, but here's a photo of my model.

Here's my simple model. The vanishing point is at the very center.

We could also put the vanishing point off-center, so that the squares or cubes aren't inside each other. That also looks weird, but different.

The lines go through the cube for clarity. The vanishing point is off to the right.

So I don't know if there really is a "best way" to show four-dimensional shapes. I personally like the perspective models better.

Animation can help, also, by letting us see how it looks as it rotates. Sadly, I don't have a way to project animation into three dimensions, so it will have to be on a screen or a page. It's good that our brains are tuned to see two-dimensional pictures as three-dimensional.

So here's our tesseract, rotating.

Made by Jason Hise, released into the public domain.

Now you can tell how those poor Flatlanders felt when they saw the rotating cube turn itself inside out.

And, just because I haven't screwed with your minds enough yet, here are the four-dimensional versions of the D&D dice. (You can also see the view from inside the "4d120".)

Enjoy! >: D