Thursday, December 13, 2012
Thursday, November 29, 2012
Script Evolution Explanation
I've been asked why I haven't continued with the script evolution project. Well, I have, but I just haven't been writing posts about it.
Until I can figure out the "diagram problem" I can't find a good way to post the iterations, and without that the posts would be meaningless.
I'll post all of the ones I've made as soon as I get the images working, though. Sorry.
Until I can figure out the "diagram problem" I can't find a good way to post the iterations, and without that the posts would be meaningless.
I'll post all of the ones I've made as soon as I get the images working, though. Sorry.
Thursday, November 15, 2012
A Musical Challenge
This post deviates quite a bit from my usual ones. Rather than researching a topic, this time I'm asking you to do the work. ; )
As some of you probably know, the Urbana Pops Orchestra just announced that they're holding a composition contest. Anyone in the East-Central Illinois area can write and orchestrate a piece for them, based on the theme "Space: A Musical Frontier." The winning over-18 entry and the winning 18-and-under entry will be performed at the concert next summer.
I've been working hard on my composition, and as such have been thinking a lot more about musical theory lately. This is an idea I had a while back, and I realized that this blog would be a good format for it.
So here's my mini-composition challenge.
Come up with a short melody based on the following chords, preferably in 4/4 time, with one bar per chord. Then I'll fit them all together and post the results.
C F G C C F G G7 Am F G C
These chords aren't very interesting, but I figured a simple example would be best to start off. I-IV-V-I and variations thereof are used for all sorts of different pieces, same with replacing an I with a vi.
If you come up with a melody from these, for whatever instrument, post it in the comments below. It'll be interesting to see what everyone comes up with!
 |
| Bach's Two-Part Invention #1, the first few bars. |
As some of you probably know, the Urbana Pops Orchestra just announced that they're holding a composition contest. Anyone in the East-Central Illinois area can write and orchestrate a piece for them, based on the theme "Space: A Musical Frontier." The winning over-18 entry and the winning 18-and-under entry will be performed at the concert next summer.
I've been working hard on my composition, and as such have been thinking a lot more about musical theory lately. This is an idea I had a while back, and I realized that this blog would be a good format for it.
So here's my mini-composition challenge.
Come up with a short melody based on the following chords, preferably in 4/4 time, with one bar per chord. Then I'll fit them all together and post the results.
These chords aren't very interesting, but I figured a simple example would be best to start off. I-IV-V-I and variations thereof are used for all sorts of different pieces, same with replacing an I with a vi.
If you come up with a melody from these, for whatever instrument, post it in the comments below. It'll be interesting to see what everyone comes up with!
Thursday, November 8, 2012
On the Non-Existance of Diagrams
Sorry, everyone, I know my images haven't been showing up in posts recently. I think I've found the problem, it seems to be a certain type of PNG file that Blogger chokes on, and I'm going to try re-exporting everything with different settings. If that doesn't work I'll *shudder* save the images as JPEGs, which I know will show up.
On the Existence of Dragons, Part II
Yet again I have more information on this, and I don't want to turn the original post into one big wall of text. So here's the third post in the "series," enjoy.
Here was my original idea for how a dragon's respiratory system could work:
[Diagram]
Rather than having one pair of lungs exchange carbon dioxide for oxygen in the blood, the dragon has two. Blood first passes through the second pair of lungs, which contain the triethylaluminum or similar, to release the carbon dioxide. Then oxygen is picked up in the first pair of lungs, as usual.
We're assuming that this blood contains a special type of hemoglobin that is unusually effective in picking up oxygen, or that the dragon continues to hold oxygen-rich air in its lungs before exhaling until all the oxygen is gone. Otherwise there might be problems.
Then, when the dragon breathes out, the CO2 and triethylaluminum come into contact with the air, and ignite. As long as the dragon doesn't breathe in until the fire's gone, it isn't at risk of burning itself.
One other problem that comes up is how the dragon can keep the two pairs of lungs separate, when they're both connected to its trachea (windpipe).
Well, humans have this problem as well, in a way. Both the lungs and the stomach are connected to the back of the throat, but are kept separate by a flap called the epiglottis. We can assume that this would work for the dragons as well, although setting yourself on fire from the inside is rather more unpleasant than coughing if something goes wrong.
Now, could we extend this to other things as well? Apparently, many folktales involve dragons that breathe out ice or poison instead of fire.
Poison is easy, many different types of animals already can create poisons and toxins.
Ice is a bit more interesting, though.
There are several types of chemical reactions that are extremely endothermic--they take energy out of their surroundings when they react, so everything nearby becomes colder. This is how cold-packs work. The best one I found is 85 grams magnesium chloride hexahydrate, MgCl2(H2O)6 (commonly used to de-ice roads) and 100 grams ice. According to one source, this reaction can bring the solution to -94 degrees Celsius (-137.2 degrees Fahrenheit)!
So rather than the modified respiratory system, this frost-breathing dragon might have a structure in its mouth in which the magnesium chloride is created, and then it could trigger the reaction by chewing on a piece of ice or snow. Hopefully it could avoid frostbite in its mouth while breathing out. But at least keeping cool wouldn't be a problem.
Here was my original idea for how a dragon's respiratory system could work:
[Diagram]
Rather than having one pair of lungs exchange carbon dioxide for oxygen in the blood, the dragon has two. Blood first passes through the second pair of lungs, which contain the triethylaluminum or similar, to release the carbon dioxide. Then oxygen is picked up in the first pair of lungs, as usual.
We're assuming that this blood contains a special type of hemoglobin that is unusually effective in picking up oxygen, or that the dragon continues to hold oxygen-rich air in its lungs before exhaling until all the oxygen is gone. Otherwise there might be problems.
Then, when the dragon breathes out, the CO2 and triethylaluminum come into contact with the air, and ignite. As long as the dragon doesn't breathe in until the fire's gone, it isn't at risk of burning itself.
One other problem that comes up is how the dragon can keep the two pairs of lungs separate, when they're both connected to its trachea (windpipe).
Well, humans have this problem as well, in a way. Both the lungs and the stomach are connected to the back of the throat, but are kept separate by a flap called the epiglottis. We can assume that this would work for the dragons as well, although setting yourself on fire from the inside is rather more unpleasant than coughing if something goes wrong.
Now, could we extend this to other things as well? Apparently, many folktales involve dragons that breathe out ice or poison instead of fire.
Poison is easy, many different types of animals already can create poisons and toxins.
Ice is a bit more interesting, though.
There are several types of chemical reactions that are extremely endothermic--they take energy out of their surroundings when they react, so everything nearby becomes colder. This is how cold-packs work. The best one I found is 85 grams magnesium chloride hexahydrate, MgCl2(H2O)6 (commonly used to de-ice roads) and 100 grams ice. According to one source, this reaction can bring the solution to -94 degrees Celsius (-137.2 degrees Fahrenheit)!
So rather than the modified respiratory system, this frost-breathing dragon might have a structure in its mouth in which the magnesium chloride is created, and then it could trigger the reaction by chewing on a piece of ice or snow. Hopefully it could avoid frostbite in its mouth while breathing out. But at least keeping cool wouldn't be a problem.
Monday, November 5, 2012
On the Existence of Dragons, Part 1.5
Just a bit more explanation, since I don't like making big changes to previous posts...
The Square-Cube Law is based on the fact that a cubic function (based on x3) will always overtake a quadratic (based on x2) function. No matter what. Even if you compare 0.01x3 and 999x2, the cubic will always "win". And they'll keep getting further and further apart the higher you go. There's no way to make them stay close together for very long.
The Square-Cube Law, then, brings this from algebra to geometry. It says that, as you scale something up, its volume increases by a cube, and its surface area by a square.
This is relevant in all sorts of different fields. For example, let's say you are designing a ship. If you take, say, a small sailboat and scale it up to the right size, it won't work at all. It might not even float, and it certainly won't be able to sail. The mass of the boat increased by the cube of the scaling factor, but the size of the sails only increased by the square.
And, as the previous post stated, this is why an elephant looks nothing like a scaled-up mouse. Strength is based on the cross-section of the muscle, which increases by a square. But mass and weight are based on the volume, which increases by a cube. As an animal is scaled up, its muscles need to be larger and larger compared to its size.
Another biological problem with this that I didn't mention is overheating. Small animals have a lot of surface area compared to volume, so they can lose heat easily through their skin. But large animals have a harder and harder time doing this. (Especially if they breathe fire.) Our dragon would at the very least have to be able to sweat to remove heat, bringing in yet another non-reptilian characteristic. But I suppose it's more likely than fire breathing at any rate.
The Square-Cube Law is based on the fact that a cubic function (based on x3) will always overtake a quadratic (based on x2) function. No matter what. Even if you compare 0.01x3 and 999x2, the cubic will always "win". And they'll keep getting further and further apart the higher you go. There's no way to make them stay close together for very long.
The Square-Cube Law, then, brings this from algebra to geometry. It says that, as you scale something up, its volume increases by a cube, and its surface area by a square.
 |
| I just took this from Google Images for now, I'll make a better version of it later. Sorry. |
And, as the previous post stated, this is why an elephant looks nothing like a scaled-up mouse. Strength is based on the cross-section of the muscle, which increases by a square. But mass and weight are based on the volume, which increases by a cube. As an animal is scaled up, its muscles need to be larger and larger compared to its size.
Another biological problem with this that I didn't mention is overheating. Small animals have a lot of surface area compared to volume, so they can lose heat easily through their skin. But large animals have a harder and harder time doing this. (Especially if they breathe fire.) Our dragon would at the very least have to be able to sweat to remove heat, bringing in yet another non-reptilian characteristic. But I suppose it's more likely than fire breathing at any rate.
Monday, October 29, 2012
On the Existence of Dragons
Here you go, Ruth. I'm actually writing about it.
In our world, it seems that dragons shouldn't be able to exist. Reptiles don't fly, don't breathe fire, and don't grow to the size of buildings.
Some of these could possibly have evolved. Dragons might have descended from the same common ancestor as bird and reptiles, and diverged at the same time; it wouldn't be impossible for them to have some features similar to modern birds and others similar to modern reptiles.
Organisms have also developed many kinds of chemicals and poisons for defense...why not something similar to triethylaluminum, which ignites upon contact with oxygen? It can be synthesized from hydrogen, aluminum, and methane, none of which is too hard to find. And maybe dragons have a way to extract more oxygen from the air in their respiratory system, so they breathe out almost pure carbon dioxide (which would prevent them setting themselves on fire).
But there's one big problem: the square-cube law.
Edit: I've made a new post about the square-cube law, look here.
The square-cube law states that, as you scale something up, the volume changes faster than the surface area. The surface area increases as the square of the length, and the volume as the cube.
If you look at a graph of the two, you can see that they keep getting further and further apart.
And this applies to biology, because strength is proportional to the cross-section of the muscle, which is an area, while mass is proportional to the volume of the animal. This is why ants can lift such heavy weights compared to their own, but we can't. If you scaled an ant up to the size of a person, its legs would snap under the weight of its own body.
This is even more of a problem for things that fly. If you scaled up an airplane to double its size, it would weigh 23=8 times as much, but it would only get 22=4 times the lift of the smaller plane. It wouldn't even be able to take off.
So let's imagine we have a very small, fire-breathing dragon, a bit smaller than a Komodo monitor. Its bones could be hollow, like a bird's, to make it lighter. It could presumably be able to fly--after all, we've seen birds approximately that size that can fly perfectly fine.
Our small dragon is about two meters long. We want the full-sized dragon to be, say, 64 meters long, 32 times longer. Its new surface area will be 1024 times its original, but its new volume will be 32,768 times larger!
So there's no way it could fly, although with enough muscle it might be able to support itself. Possibly.
Or are we missing something?
Now I'm going to deviate completely from reality, so you might want to read the previous two posts first.
Imagine that we have a fold in the world, but not a complete one like in the previous posts. Only a partial one. This dragon could essentially create a little "ledge" for itself, in which gravity would be reduced or even negated.
Now it would have no problems! There are animals larger than it on Earth which survive just fine--blue whales, because they live in the water. The buoyant force essentially weakens gravity, so they can move however they want in three dimensions.
Let's assume, however, that our dragon is purely three-dimensional. I don't even want to try analyzing the "cube-tesseract law."
TL;DR: It's perfectly possible that dragons exist, even though the square-cube law still holds. They could even fly and breathe fire.
 |
| A statue of two dragons in Varna. |
In our world, it seems that dragons shouldn't be able to exist. Reptiles don't fly, don't breathe fire, and don't grow to the size of buildings.
Some of these could possibly have evolved. Dragons might have descended from the same common ancestor as bird and reptiles, and diverged at the same time; it wouldn't be impossible for them to have some features similar to modern birds and others similar to modern reptiles.
Organisms have also developed many kinds of chemicals and poisons for defense...why not something similar to triethylaluminum, which ignites upon contact with oxygen? It can be synthesized from hydrogen, aluminum, and methane, none of which is too hard to find. And maybe dragons have a way to extract more oxygen from the air in their respiratory system, so they breathe out almost pure carbon dioxide (which would prevent them setting themselves on fire).
But there's one big problem: the square-cube law.
Edit: I've made a new post about the square-cube law, look here.
The square-cube law states that, as you scale something up, the volume changes faster than the surface area. The surface area increases as the square of the length, and the volume as the cube.
If you look at a graph of the two, you can see that they keep getting further and further apart.
And this applies to biology, because strength is proportional to the cross-section of the muscle, which is an area, while mass is proportional to the volume of the animal. This is why ants can lift such heavy weights compared to their own, but we can't. If you scaled an ant up to the size of a person, its legs would snap under the weight of its own body.
This is even more of a problem for things that fly. If you scaled up an airplane to double its size, it would weigh 23=8 times as much, but it would only get 22=4 times the lift of the smaller plane. It wouldn't even be able to take off.
So let's imagine we have a very small, fire-breathing dragon, a bit smaller than a Komodo monitor. Its bones could be hollow, like a bird's, to make it lighter. It could presumably be able to fly--after all, we've seen birds approximately that size that can fly perfectly fine.
Our small dragon is about two meters long. We want the full-sized dragon to be, say, 64 meters long, 32 times longer. Its new surface area will be 1024 times its original, but its new volume will be 32,768 times larger!
So there's no way it could fly, although with enough muscle it might be able to support itself. Possibly.
Or are we missing something?
Now I'm going to deviate completely from reality, so you might want to read the previous two posts first.
Imagine that we have a fold in the world, but not a complete one like in the previous posts. Only a partial one. This dragon could essentially create a little "ledge" for itself, in which gravity would be reduced or even negated.
Now it would have no problems! There are animals larger than it on Earth which survive just fine--blue whales, because they live in the water. The buoyant force essentially weakens gravity, so they can move however they want in three dimensions.
Let's assume, however, that our dragon is purely three-dimensional. I don't even want to try analyzing the "cube-tesseract law."
TL;DR: It's perfectly possible that dragons exist, even though the square-cube law still holds. They could even fly and breathe fire.
Tuesday, October 23, 2012
Quick Follow-Up
A few more things about the Gravity and Portals post...
One of the What-If.xkcd.com answers recently concerned airflow through portals. According to Randall's answer, the flow rate through portals in Mexico City and Boston would be about 440 mph.
The same thing would happen with our world-folding portals, assuming that you moved the air along with everything else. Maybe there are transparent walls on the "front" and "back" of our world in the fourth dimension?
[Stupid diagrams! Upload!]
This seems like it would pose a problem, if we had a very (very very) tall room.
But remember, we would still have to fold it. That takes quite a bit of energy, which is proportional to the square of the height (remember, Wnet = F Δx = mworld g Δx, and the mass of part of a uniformly-dense world would be proportional to the volume we lift).
We're already using a LOT of energy in our folding, so let's assume the mass-to-energy-converter in our portal gun can't quite lift enough of the world to make a significant difference in air pressure. Portals on the moon are right out.
One of the What-If.xkcd.com answers recently concerned airflow through portals. According to Randall's answer, the flow rate through portals in Mexico City and Boston would be about 440 mph.
The same thing would happen with our world-folding portals, assuming that you moved the air along with everything else. Maybe there are transparent walls on the "front" and "back" of our world in the fourth dimension?
[Stupid diagrams! Upload!]
This seems like it would pose a problem, if we had a very (very very) tall room.
But remember, we would still have to fold it. That takes quite a bit of energy, which is proportional to the square of the height (remember, Wnet = F Δx = mworld g Δx, and the mass of part of a uniformly-dense world would be proportional to the volume we lift).
We're already using a LOT of energy in our folding, so let's assume the mass-to-energy-converter in our portal gun can't quite lift enough of the world to make a significant difference in air pressure. Portals on the moon are right out.
Thursday, October 18, 2012
Gravity and Portals
As you might be able to guess, I've been playing quite a bit of Portal 2 recently.
If you haven't played it, it's a physics-puzzle-based game where you have the ability to create portals on certain surfaces.
These portals act quite a bit like the ones I mentioned in my earlier post, where you could "fold" the two-dimensional world.
But the problem with the portals in the game is that they break the Laws of Thermodynamics. These are a set of rules about how energy works, which can be reduced to this:
So what happens if you have portals to work with?
You can create energy by teleporting up to a ledge, which gives you more gravitational potential energy. Normally you would have to convert kinetic (motion) energy in order to get up there, which makes up for it. But if you can teleport, then that restriction is gone!
And you can also destroy energy, which should also be impossible. Say you step on a Faith Plate, a catapult-like thing that launches you upwards. The catapult converts potential energy from its battery or power source into kinetic energy, which it then imparts on you. That all works. Let's say you land on a ledge at the top. When you hit the ledge, your energy is transferred to it. Still following the laws.
But what if you place a portal underneath you at the top? Now you're at the bottom again...but where did all the potential energy go? It's just gone!
[Images Pending, Sorry]
But wait a minute.
The third law says that there's no way to break either of the first two. Did we just get around that? Is our test subject freezing to death in a room colder than outer space?
It makes more sense if you look at a two-dimensional Flatlander doing the same thing. Let's turn Flatland on its edge, so that we can see the effects of gravity.
Now, when we make our first portal up to the ledge, what happens?
There's our answer! We didn't actually gain potential energy at all--because when the portal is open, the two places are at exactly the same height!
When we created the portal, we actually lifted up the lower part of the universe, and that's where the energy came from.
And, if our Flatlander jumps off the ledge to use some of that energy, then gravity starts acting strangely...when they're in the "folded" part, there seems to be no gravity at all. That's not what we see in Portal 2, although it might be interesting if we did.
Now, when we close the portal, we open out the universe again, and everything goes back to normal.
So what about the second example? Can we still destroy energy?
As it turns out, no. Let's say we open the portal when our little test subject is at the peak of their trajectory, about to land.
[Images Pending, Sorry]
Since we lifted up half of their world, they didn't lose any energy. Hitting the ground below was the same as if they hadn't used a portal at all.
But when we CLOSE the portal, and set everything back to normal, then there's a release of energy. And since we set down a little bit more than we lifted up (since the Flatlander wasn't in the area we folded the first time), that's where the extra energy goes.
So that makes sense now, although gravity still behaves strangely around portals.
If the test subject jumps off a high platform, hopefully above something soft, then what happens when we open a portal?
To us it looks like they fall straight down, but to them gravity has suddenly broken. I've used a bit of hacking to show what it would look like in the video game itself. (This also shows the examples I was talking about.)
Strange, no? I can see why Valve didn't build their game this way. Maybe that portal gun contains a nuclear battery or some other small power source, which can not only provide enough power to fold the universe but which can change the effects of gravity (look at the effect when you hold a cube).
If you haven't played it, it's a physics-puzzle-based game where you have the ability to create portals on certain surfaces.
These portals act quite a bit like the ones I mentioned in my earlier post, where you could "fold" the two-dimensional world.
But the problem with the portals in the game is that they break the Laws of Thermodynamics. These are a set of rules about how energy works, which can be reduced to this:
- You can't get out more than you put in--there's no way to create or destroy energy.
- You can't even get back just what you put in--a little bit spreads out into the universe. More subtly, some things are irreversible. If a perpetual motion machine fails because friction keeps turning some energy into heat, you can't put it in a box and extract that heat again in a useful way.
- You can't break either of the first two rules. Ever. Under any circumstances. The only way you could do it would be to lower a perfect crystal to absolute zero, and this law says that's impossible*.
So what happens if you have portals to work with?
You can create energy by teleporting up to a ledge, which gives you more gravitational potential energy. Normally you would have to convert kinetic (motion) energy in order to get up there, which makes up for it. But if you can teleport, then that restriction is gone!
And you can also destroy energy, which should also be impossible. Say you step on a Faith Plate, a catapult-like thing that launches you upwards. The catapult converts potential energy from its battery or power source into kinetic energy, which it then imparts on you. That all works. Let's say you land on a ledge at the top. When you hit the ledge, your energy is transferred to it. Still following the laws.
But what if you place a portal underneath you at the top? Now you're at the bottom again...but where did all the potential energy go? It's just gone!
[Images Pending, Sorry]
But wait a minute.
The third law says that there's no way to break either of the first two. Did we just get around that? Is our test subject freezing to death in a room colder than outer space?
It makes more sense if you look at a two-dimensional Flatlander doing the same thing. Let's turn Flatland on its edge, so that we can see the effects of gravity.
Now, when we make our first portal up to the ledge, what happens?
There's our answer! We didn't actually gain potential energy at all--because when the portal is open, the two places are at exactly the same height!
When we created the portal, we actually lifted up the lower part of the universe, and that's where the energy came from.
And, if our Flatlander jumps off the ledge to use some of that energy, then gravity starts acting strangely...when they're in the "folded" part, there seems to be no gravity at all. That's not what we see in Portal 2, although it might be interesting if we did.
Now, when we close the portal, we open out the universe again, and everything goes back to normal.
So what about the second example? Can we still destroy energy?
As it turns out, no. Let's say we open the portal when our little test subject is at the peak of their trajectory, about to land.
[Images Pending, Sorry]
Since we lifted up half of their world, they didn't lose any energy. Hitting the ground below was the same as if they hadn't used a portal at all.
But when we CLOSE the portal, and set everything back to normal, then there's a release of energy. And since we set down a little bit more than we lifted up (since the Flatlander wasn't in the area we folded the first time), that's where the extra energy goes.
So that makes sense now, although gravity still behaves strangely around portals.
If the test subject jumps off a high platform, hopefully above something soft, then what happens when we open a portal?
 |
| Left: what we 3-dimensional beings can see. Right: What it looks like to a test subject. |
To us it looks like they fall straight down, but to them gravity has suddenly broken. I've used a bit of hacking to show what it would look like in the video game itself. (This also shows the examples I was talking about.)
Strange, no? I can see why Valve didn't build their game this way. Maybe that portal gun contains a nuclear battery or some other small power source, which can not only provide enough power to fold the universe but which can change the effects of gravity (look at the effect when you hold a cube).
Thursday, October 4, 2012
One-Point Perspective
People seemed to like my first post about the fourth dimension, so I'm going to attempt to write another. This one gave me a migraine when I first started thinking about it, so be warned.
As you might remember from geometry classes, there are five "Platonic Solids" in three dimensions. These are objects that are made up of a single two-dimensional polygon, repeated and connected. In math terms, they're the tetrahedron, the cube, the octahedron, the dodecahedron, and the icosahedron. In geek terms, they're the d4, the d6, the d8, the d12, and the d20. They're named after Plato, who believed that the four elements of the universe were made up of little pieces, shaped like these solids. Water was the icosahedron, which is almost spherical and can roll around. Fire was the tetrahedron, which has sharp corners and is only stable with a point facing upwards. Earth was the cube, which can be packed together into bigger cubes without space between them. And air was the octahedron, for no real reason. (The dodecahedron was left out of this theory. It's now best known as the D&D die that nobody ever uses, the d12.)
If you think about it, these could be considered the 3-dimensional equivalents to regular polygons--shapes where every edge is the same length, such as a square or an equilateral triangle. So could there be four-dimensional equivalents, built out of 3-dimensional solids?
The easiest one to think about is the cube, so I'll just focus on that one for now.
The cube can be thought of as part of a series, going up through dimensions: in one dimension there's the line segment, in two dimensions the square, in three the cube, and...so on? The four-dimensional one is sometimes called the 4-hypercube, or tesseract.
Now, if you start from the one-dimensional line segment, you can form a square by duplicating the segment, then connecting them. So if we start with a one-inch line segment pointing forward-backward, we can place another segment an inch to the right, and connect the endpoints.
That gets a square. And we can repeat the process to make a cube: place another square an inch above the first, and connect the endpoints.
To make a tesseract, then, it would seem that you could just place another cube one inch along the fourth dimension, and connect the lines. That makes theoretical sense...but what would it look like, if you actually created one? To figure that out, we can turn to perspective.
Generally perspective is used to portray a three-dimensional object in two dimensions, by stretching and skewing parts of it.
If we took a folded paper cube, made of six squares, we could show it to a Flatland being by placing the six squares next to each other--"unfolding" it into a cross shape.
And we can do the same for the eight cubes of the tesseract.
Salvador Dali once made a painting based on this net.
But this picture doesn't help us very much. I, for one, can't really tell anything about what the finished tesseract would look like from seeing the arrangement of cubes there, even though I can see what shapes comprise it.
So the other way to show it to the Flatlanders would be to use perspective.
If you look at the picture, you can imagine the cubes being there, although of course it's two-dimensional. But if you tell the Flatlanders that each cube made of six squares, they will probably be very confused. Looking at the picture, one can see six rhombuses, but only two actual squares (the front and back). The other four are distorted by the perspective. And if you somehow animated your drawing to make the cube rotate, it would blow their minds. Somehow these squares are becoming rhombuses, and passing through each other, and even changing in size! But somehow this is supposed to be a solid object?
It might be easiest to draw the cube with perspective using one-point perspective, where every line leads to a single vanishing point. [The cube on the right.]
You can still see that this is a cube, although it's less clear than some other ways of drawing it.
I was thinking a few days ago that this form of perspective could also possibly be applied to a four-dimensional object. One-point perspective is probably the easiest to make. But somehow it will need to be applied to a three-dimensional object...
Looking at the cube, it looks like a smaller square inside a bigger square, with diagonal lines representing the third dimension.
So, why not try that with our tesseract?
Unfortunately, I can only upload two-dimensional pictures onto this blog, but here's a photo of my model.
We could also put the vanishing point off-center, so that the squares or cubes aren't inside each other. That also looks weird, but different.
So I don't know if there really is a "best way" to show four-dimensional shapes. I personally like the perspective models better.
Animation can help, also, by letting us see how it looks as it rotates. Sadly, I don't have a way to project animation into three dimensions, so it will have to be on a screen or a page. It's good that our brains are tuned to see two-dimensional pictures as three-dimensional.
So here's our tesseract, rotating.
Now you can tell how those poor Flatlanders felt when they saw the rotating cube turn itself inside out.
And, just because I haven't screwed with your minds enough yet, here are the four-dimensional versions of the D&D dice. (You can also see the view from inside the "4d120".)
Enjoy! >: D
As you might remember from geometry classes, there are five "Platonic Solids" in three dimensions. These are objects that are made up of a single two-dimensional polygon, repeated and connected. In math terms, they're the tetrahedron, the cube, the octahedron, the dodecahedron, and the icosahedron. In geek terms, they're the d4, the d6, the d8, the d12, and the d20. They're named after Plato, who believed that the four elements of the universe were made up of little pieces, shaped like these solids. Water was the icosahedron, which is almost spherical and can roll around. Fire was the tetrahedron, which has sharp corners and is only stable with a point facing upwards. Earth was the cube, which can be packed together into bigger cubes without space between them. And air was the octahedron, for no real reason. (The dodecahedron was left out of this theory. It's now best known as the D&D die that nobody ever uses, the d12.)
If you think about it, these could be considered the 3-dimensional equivalents to regular polygons--shapes where every edge is the same length, such as a square or an equilateral triangle. So could there be four-dimensional equivalents, built out of 3-dimensional solids?
The easiest one to think about is the cube, so I'll just focus on that one for now.
The cube can be thought of as part of a series, going up through dimensions: in one dimension there's the line segment, in two dimensions the square, in three the cube, and...so on? The four-dimensional one is sometimes called the 4-hypercube, or tesseract.
Now, if you start from the one-dimensional line segment, you can form a square by duplicating the segment, then connecting them. So if we start with a one-inch line segment pointing forward-backward, we can place another segment an inch to the right, and connect the endpoints.
That gets a square. And we can repeat the process to make a cube: place another square an inch above the first, and connect the endpoints.
To make a tesseract, then, it would seem that you could just place another cube one inch along the fourth dimension, and connect the lines. That makes theoretical sense...but what would it look like, if you actually created one? To figure that out, we can turn to perspective.
Generally perspective is used to portray a three-dimensional object in two dimensions, by stretching and skewing parts of it.
If we took a folded paper cube, made of six squares, we could show it to a Flatland being by placing the six squares next to each other--"unfolding" it into a cross shape.
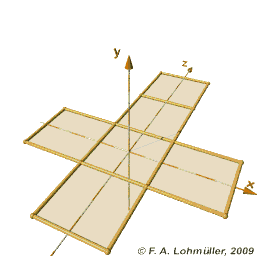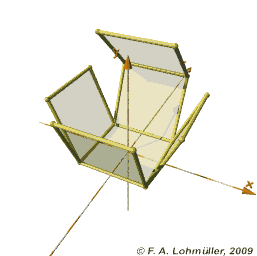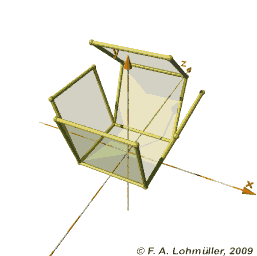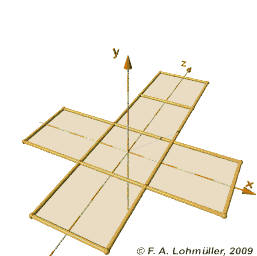 |
| I didn't make this image, I'm bad at 3d animation. |
And we can do the same for the eight cubes of the tesseract.
| Nor this one, sorry. |
Salvador Dali once made a painting based on this net.
But this picture doesn't help us very much. I, for one, can't really tell anything about what the finished tesseract would look like from seeing the arrangement of cubes there, even though I can see what shapes comprise it.
So the other way to show it to the Flatlanders would be to use perspective.
If you look at the picture, you can imagine the cubes being there, although of course it's two-dimensional. But if you tell the Flatlanders that each cube made of six squares, they will probably be very confused. Looking at the picture, one can see six rhombuses, but only two actual squares (the front and back). The other four are distorted by the perspective. And if you somehow animated your drawing to make the cube rotate, it would blow their minds. Somehow these squares are becoming rhombuses, and passing through each other, and even changing in size! But somehow this is supposed to be a solid object?
 |
| If it doesn't rotate, click it. Note: I didn't make this! |
It might be easiest to draw the cube with perspective using one-point perspective, where every line leads to a single vanishing point. [The cube on the right.]
You can still see that this is a cube, although it's less clear than some other ways of drawing it.
I was thinking a few days ago that this form of perspective could also possibly be applied to a four-dimensional object. One-point perspective is probably the easiest to make. But somehow it will need to be applied to a three-dimensional object...
Looking at the cube, it looks like a smaller square inside a bigger square, with diagonal lines representing the third dimension.
So, why not try that with our tesseract?
Unfortunately, I can only upload two-dimensional pictures onto this blog, but here's a photo of my model.
 |
| Here's my simple model. The vanishing point is at the very center. |
We could also put the vanishing point off-center, so that the squares or cubes aren't inside each other. That also looks weird, but different.
 |
| The lines go through the cube for clarity. The vanishing point is off to the right. |
So I don't know if there really is a "best way" to show four-dimensional shapes. I personally like the perspective models better.
Animation can help, also, by letting us see how it looks as it rotates. Sadly, I don't have a way to project animation into three dimensions, so it will have to be on a screen or a page. It's good that our brains are tuned to see two-dimensional pictures as three-dimensional.
So here's our tesseract, rotating.
 |
| Made by Jason Hise, released into the public domain. |
And, just because I haven't screwed with your minds enough yet, here are the four-dimensional versions of the D&D dice. (You can also see the view from inside the "4d120".)
Enjoy! >: D
Wednesday, September 19, 2012
Script Evolution, Part 0
This is just going to be a short post, about an idea that I had had recently.
As I've probably said before, I've always been interested in different writing systems. So as soon as I saw the "tengwar" script on the cover of the Fellowship of the Ring, I started looking for more information on it.
I discovered that Tolkein, as a perfectionist, wanted his writing systems to seem as real as possible. He had created a "base" script for the tengwar, and slowly evolved it into the modern version, imitating the way that real forms of writing change over time. I thought this sounded like a very interesting idea, and I wanted to try it as an experiment.
So here's a simple idea for a writing system that I came up with recently. The letters are simple geometric shapes, and they're arranged into syllables as in Hangul (the Korean alphabet).
Every couple weeks I will try to write something out over and over in the script. Certain features should hopefully start to change over time.
So here's the script as it starts out.
I tried to make it straight and angular, as the Latin alphabet originally was (to make it easier to carve into stone, mostly). The vowels O and U were added to the fictional language later, and have more rounded shapes. And the shapes will probably become more rounded through their "evolution", just as A became a and M became m for us.
The alphabet is phonetic, so it doesn't quite match the English alphabet. Most of the letters are pronounced just as you'd expect, except:
- ʔ - the "glottal stop" that occasionally replaces the "t" sound in "button", uncommon. Many "t"s are replaced by this letter in Australian and Cockney dialects.
- Ŋ (next to N and M, if it doesn't show up) - the "ng" sound in the word "singing"
- Þ - the "th" sound in the word "thin", which looked like a "y" in Old English (thus "ye olde...", which is supposed to be "the")
- Ð - the "th" sound in the word "this", slightly different from Þ. Compare ether (using Þ) and either (using Ð)
- X - the "ch" in many German and Scottish words, such as loch. In German, this can be used for both the ich-Laut and the ach-Laut sounds.
- ʃ - not an integral (∫), this is the "sh" sound in "shine"
- ʒ - sometimes spelled "zh", the si sound in "vision" and the s in "measure"
- Y - Used as a vowel here, not a consonant. It doesn't actually appear in English, but has a letter in several other languages: ü in German, u in French, and υ in Classical Greek. Close to the vowel in "seen".
In this script, those groups are arranged into blocks. The initial block is in the top left, the vowels in the top right, and the final block along the bottom. (See the diagram).
Wow, I wrote a lot more about that than I had expected. Since a lot of the "evolving" involves simplification, the next iteration should be a lot simpler.
As a final thought, here are the first two lines of a poem by a well-known author. I've used the letter "i" for consonantal y when necessary, and the rest of the vowels are exactly as in the original poem.
See if you can figure out what poem it is. Leave a comment if you can find the title and author. :)
Wednesday, September 5, 2012
Shapeshifting and the Fourth Dimension
Earlier in the summer, I was talking (well, emailing) with one of my friends about a possible scientific explanation for lycanthropy or shapeshifting, using a fourth spatial dimension.
As you probably know, the world we live in already has four dimensions - 0 is time, 1 is forwards-backwards, 2 is left-right, and 3 is up-down. (I'm going to ignore time from now on, since I'm talking specifically about spatial dimensions.)
However, there's been research done on additional dimensions, with string theory saying that there might be nine or more. Obviously we can't see any more dimensions, but people have come up with metaphors for explaining this. One of the most famous is the book "Flatland", narrated by a square living in a supposedly two-dimensional universe. People are polygons, the higher classes having more sides, and buildings are made of several line segments in a pattern.
When a three-dimensional person comes to the narrator's house, he's able to use that additional dimension to move through walls by stepping over them, and can become "invisible" by just being above the world, or somehow seal a door shut by putting a nail through from top to bottom.
He can even create "portals" for them, by literally folding the world and pushing them through what's now empty space. This was one explanation for how neutrinos seemed to move faster than light - they moved at their normal speed, but took a "shortcut" through a higher dimension.
A four-dimensional being would theoretically be able to do the same things in our world as we could in Flatland. However, there are other interesting ways that the fourth dimension could apply.
What if the fourth dimension did exist, but nobody could directly affect it or move through it? We might actually be four-dimensional, just like A. Square might actually be a cube in the third dimension, but unaware of it. But we might not be the same at each "cross-section"...
In this example, a 3-dimensional shape has a square at one cross-section and a triangle at another. If something forced it to shift one way or another, it would seem to everyone in Flatland that it was changing shape. At the bottom, there's a sketch for what would happen if it had an infinite number of forms. It would appear as a long rod stretching out to infinity in both directions, and every few inches along the length it might have a different cross-section.
If that were true for people, in the fourth dimension, then it would be possible (by some mysterious force...) to change shape, by shifting through the fourth dimension to a different three-dimensional "cross-section". This could also allow teleportation and invisibility of a sort, as explained before.
Ridiculously improbable, of course, but mathematically possible.
As you probably know, the world we live in already has four dimensions - 0 is time, 1 is forwards-backwards, 2 is left-right, and 3 is up-down. (I'm going to ignore time from now on, since I'm talking specifically about spatial dimensions.)
However, there's been research done on additional dimensions, with string theory saying that there might be nine or more. Obviously we can't see any more dimensions, but people have come up with metaphors for explaining this. One of the most famous is the book "Flatland", narrated by a square living in a supposedly two-dimensional universe. People are polygons, the higher classes having more sides, and buildings are made of several line segments in a pattern.
 |
| A square from Flatland and his house, as seen from above by a three-dimensional observer. |
When a three-dimensional person comes to the narrator's house, he's able to use that additional dimension to move through walls by stepping over them, and can become "invisible" by just being above the world, or somehow seal a door shut by putting a nail through from top to bottom.
He can even create "portals" for them, by literally folding the world and pushing them through what's now empty space. This was one explanation for how neutrinos seemed to move faster than light - they moved at their normal speed, but took a "shortcut" through a higher dimension.
 |
| This is also how the teleportation works in "A Wrinkle In Time". |
A four-dimensional being would theoretically be able to do the same things in our world as we could in Flatland. However, there are other interesting ways that the fourth dimension could apply.
What if the fourth dimension did exist, but nobody could directly affect it or move through it? We might actually be four-dimensional, just like A. Square might actually be a cube in the third dimension, but unaware of it. But we might not be the same at each "cross-section"...
 |
| This was my original "explanation" for how it might work, using the two-dimensional metaphor. |
 |
| [Click the image if it isn't animating] |
If that were true for people, in the fourth dimension, then it would be possible (by some mysterious force...) to change shape, by shifting through the fourth dimension to a different three-dimensional "cross-section". This could also allow teleportation and invisibility of a sort, as explained before.
Ridiculously improbable, of course, but mathematically possible.
pןɹoʍ oןןǝɥ
Hello everyone!
I just started this blog, so I don't know what my typical posts are going to be like, but I plan to post about interesting things that I do and ideas that I have. Hopefully it will be interesting to read.
If you're wondering about the upside-down title, when I was really young I thought it was interesting to look at writing in different ways, and I taught myself to read and write upside down, mirrored, and reversed. Obviously given the limited alphabet of the English language it's difficult to type upside down, but the International Phonetic Alphabet includes several letters that resemble inverted versions of Roman lowercase letters. For example, the inverted v in the title represents the vowel in the word "cut", the inverted e or schwa is the short vowel in the first syllable of "about", and the inverted r is the English "r" sound (as opposed to a capital R for the French uvular trill, or a normal lowercase r for the Spanish and Italian alveolar trill). When I was trying to think of a good title for the blog, I had an IPA chart open in one of my browser tabs, and I noticed that the letter ʌ closely resembled an inverted v (although it's supposed to be a small A without a crossbar). I saw that several other letters could be "turned" like that, such as using u for n and ı (Turkish dotless i) for i, and I had the idea for the title.
(TL;DR: the title of the blog uses IPA letters to resemble inverted Latin letters.)
Anyway, as you can see, I can sometimes wall-of-text when writing about a topic, and I'll try not to do that too much. I do a lot of science, math, linguistics, and programming stuff, but hopefully my posts won't get too technical.
I hope you find my future writing to be interesting!
I just started this blog, so I don't know what my typical posts are going to be like, but I plan to post about interesting things that I do and ideas that I have. Hopefully it will be interesting to read.
If you're wondering about the upside-down title, when I was really young I thought it was interesting to look at writing in different ways, and I taught myself to read and write upside down, mirrored, and reversed. Obviously given the limited alphabet of the English language it's difficult to type upside down, but the International Phonetic Alphabet includes several letters that resemble inverted versions of Roman lowercase letters. For example, the inverted v in the title represents the vowel in the word "cut", the inverted e or schwa is the short vowel in the first syllable of "about", and the inverted r is the English "r" sound (as opposed to a capital R for the French uvular trill, or a normal lowercase r for the Spanish and Italian alveolar trill). When I was trying to think of a good title for the blog, I had an IPA chart open in one of my browser tabs, and I noticed that the letter ʌ closely resembled an inverted v (although it's supposed to be a small A without a crossbar). I saw that several other letters could be "turned" like that, such as using u for n and ı (Turkish dotless i) for i, and I had the idea for the title.
(TL;DR: the title of the blog uses IPA letters to resemble inverted Latin letters.)
Anyway, as you can see, I can sometimes wall-of-text when writing about a topic, and I'll try not to do that too much. I do a lot of science, math, linguistics, and programming stuff, but hopefully my posts won't get too technical.
I hope you find my future writing to be interesting!
Subscribe to:
Comments (Atom)





